회귀분석은 일련의 입력값("독립 변수")에서 수치적 결과("종속 변수")를 예측하는 방법
통계적 의미: 결과의 기대값을 예측합니다.
인과적 의미: 수치적 결과를 예측하며, 범주형 결과가 아닙니다.
Q. "우리가 판매할 제품의 수량은 얼마나 되는지?" (회귀)
Q. "이 고객이 우리 제품을 구매할까? (예/아니오)" (분류)
Q. "고객이 우리 제품에 지불할 가격은 얼마인지?" (회귀)
머신러닝에서의 회귀는 다음과 같은 두 가지 관점으로 접근할 수 있습니다:
# 과학적 마인드셋(Scientific mindset): 데이터 생성 과정을 이해하기 위해 모델링합니다.
# 공학적 마인드셋(Engineering mindset): 정확한 예측을 위해 모델링합니다.
머신러닝은 주로 공학적 마인드셋에 초점을 맞춥니다.
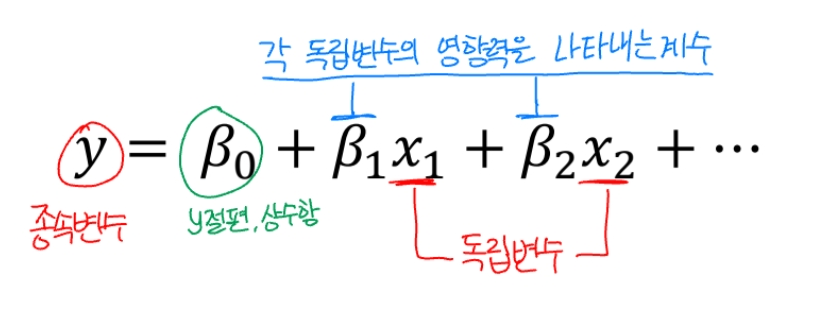
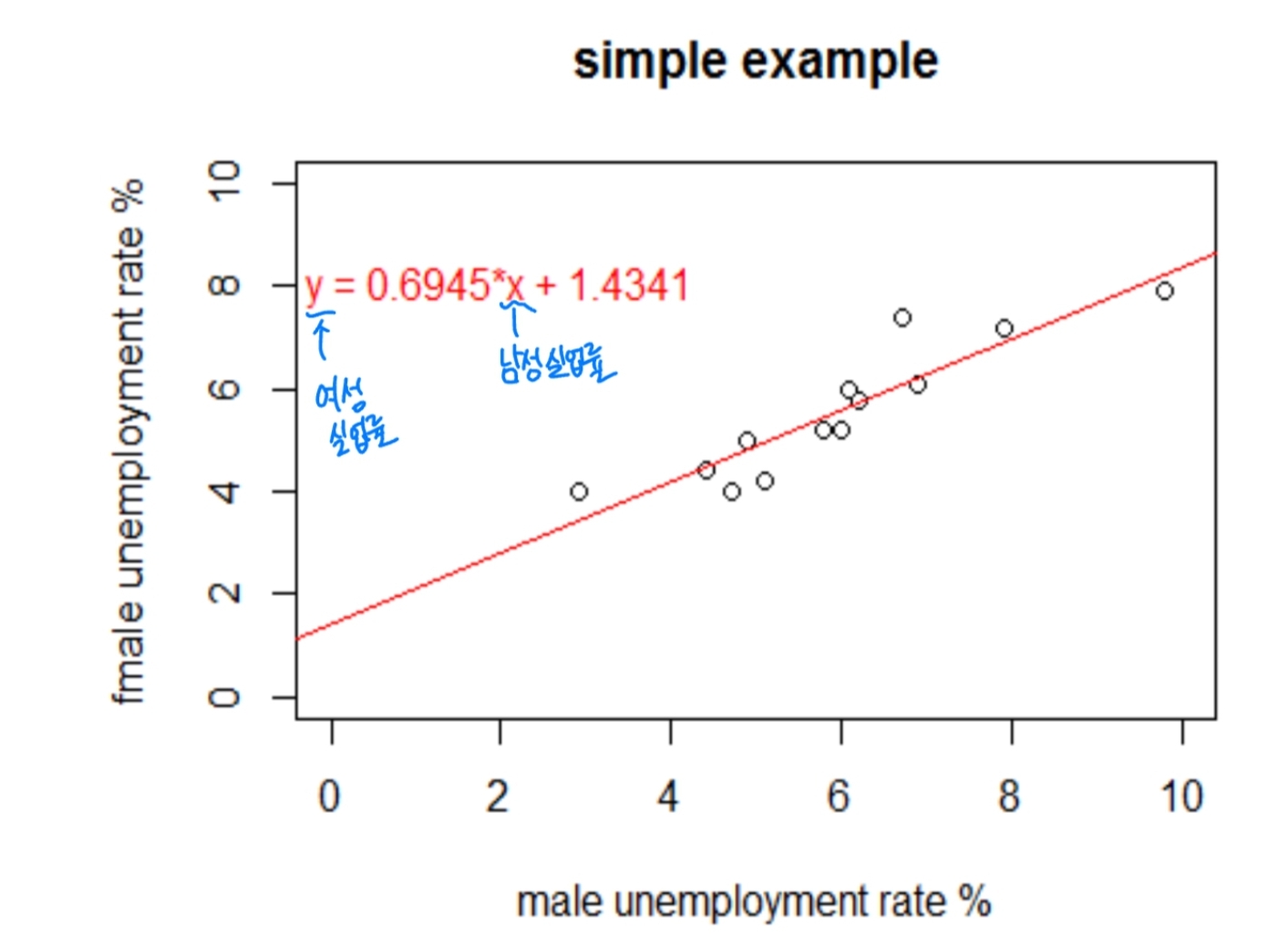
코드 적용
model <- lm(formula, data = data frame)
평가지표
- 평균제곱오차 (MSE, Mean Squared Error):
- 실제 값과 예측 값의 차이를 제곱한 후 평균을 낸 값입니다.
MSE는 값이 낮을수록 모델의 성능이 좋다는 것을 의미합니다.
- 실제 값과 예측 값의 차이를 제곱한 후 평균을 낸 값입니다.
- 루트 평균제곱오차 (RMSE, Root Mean Squared Error):
- MSE에 루트를 적용한 값입니다. RMSE는 MSE와 마찬가지로 낮을수록 좋으며,
값의 스케일이 실제 데이터의 스케일과 유사하기 때문에 해석하기가 더 쉬울 수 있습니다.
- MSE에 루트를 적용한 값입니다. RMSE는 MSE와 마찬가지로 낮을수록 좋으며,
- 결정계수 (R², R-squared):
- 모델이 데이터의 변동성을 얼마나 잘 설명하는지를 나타내는 지표입니다.
0에서 1 사이의 값을 가지며, 값이 클수록 모델의 설명력이 높다고 할 수 있습니다.
- 모델이 데이터의 변동성을 얼마나 잘 설명하는지를 나타내는 지표입니다.
- 조정 결정계수 (Adjusted R-squared):
- 독립 변수의 수가 많아질수록 단순 R²가 과대평가될 수 있는 문제를 해결하기 위해 사용됩니다.
조정 결정계수는 독립 변수의 수와 표본 크기를 고려하여 결정계수를 조정한 값입니다.
- 독립 변수의 수가 많아질수록 단순 R²가 과대평가될 수 있는 문제를 해결하기 위해 사용됩니다.
'데이터 공부' 카테고리의 다른 글
| #8 Odds and Log(Odds), 오즈와 로그오즈에 대해 (1) | 2024.06.11 |
|---|---|
| #6 나이브 베이즈(Naive Bayes)와 베이즈 정리(Bayes Theorem) (0) | 2024.06.10 |
| #5 (KNN) k-Nearest Neighbors (1) | 2024.06.10 |
| #4 Deicison Tree Model (의사결정나무) (1) | 2024.06.10 |
| #3 RMSE와 R^2에 대해 (1) | 2024.06.09 |



